Learn more about all the notebooks experiences from Microsoft and GitHub
You can enjoy powerful, integrated Jupyter notebooks with the following products and services from Microsoft and GitHub.

Notebooks in Visual Studio Code
VS Code is a free code editor and development platform that you can use locally or connected to remote compute. Combined with the Jupyter extension, it offers a full environment for Jupyter development that can be enhanced with additional language extensions. If you want a best-in-class, free Jupyter experience with the ability to leverage your compute of choice, this is a great option.
Using VS Code, you can develop and run notebooks against remotes and containers. To make the transition easier from Azure Notebooks, we have made the container image available so it can use with VS Code too.
GitHub Codespaces
GitHub Codespaces provides cloud-hosted environments where you can edit your notebooks using Visual Studio Code or your web browser and store them on GitHub. GitHub Codespaces offers the same great Jupyter experience as VS Code, but without needing to install anything on your device. GitHub Codespaces also allows you to use your cloud compute of choice.
If you don’t want to set up a local environment and prefer a cloud-backed solution, then creating a codespace is a great option.

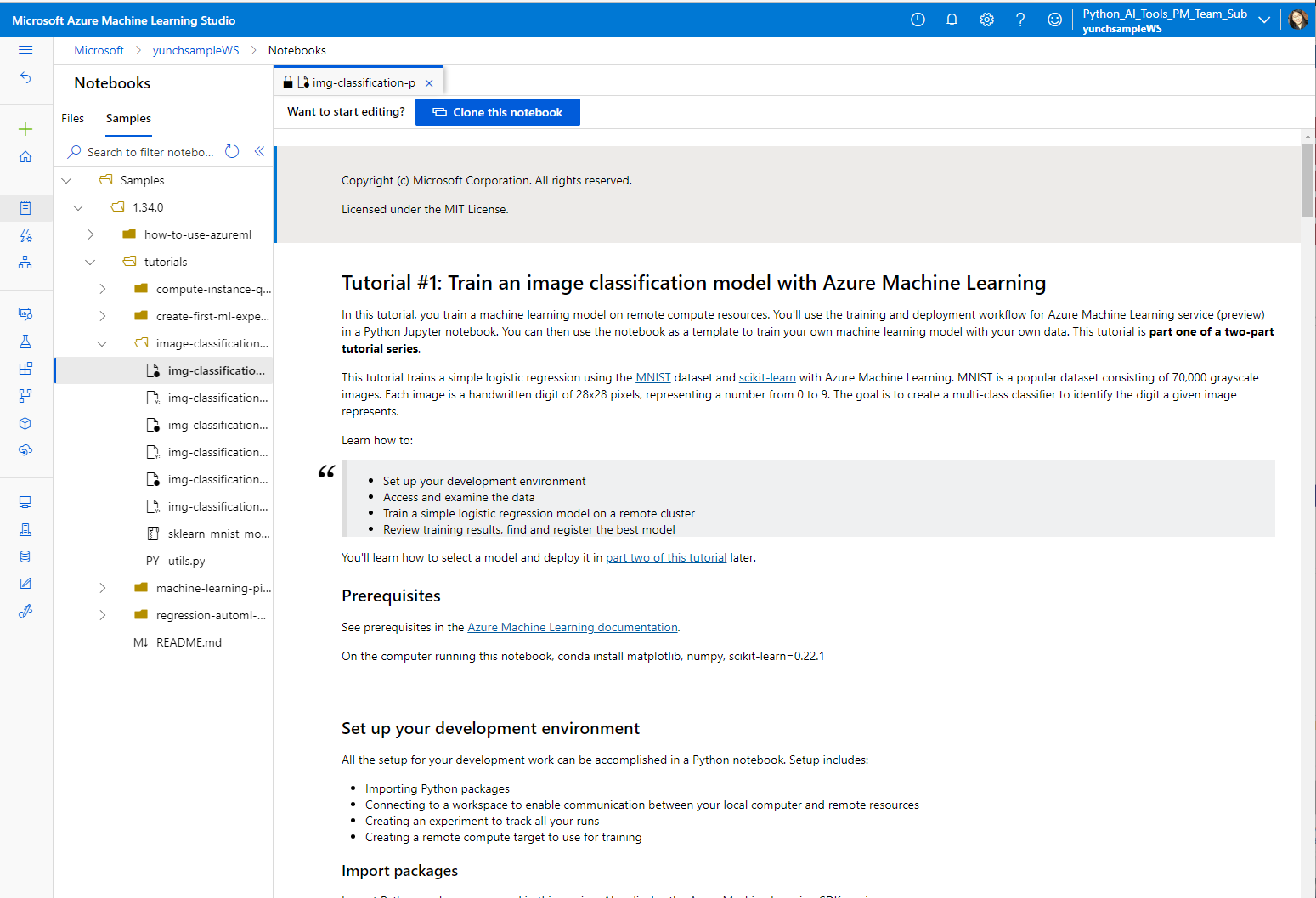
Azure Machine Learning
Azure Machine Learning provides an end-to-end machine learning platform to enable users to build and deploy models faster on Azure. Azure ML allows you to run notebooks on a VM or a shared cluster computing environment.
If you are in need of a cloud-based solution for your ML workload with experiment tracking, dataset management, and more, we recommend Azure Machine Learning.
Azure Lab Services
Azure Lab Services allows educators to easily setup and provide on-demand access to preconfigured VMs for an entire classroom.
For educators looking for a way to work with notebooks and cloud compute in a tailored classroom environment, Lab Services is a great option.

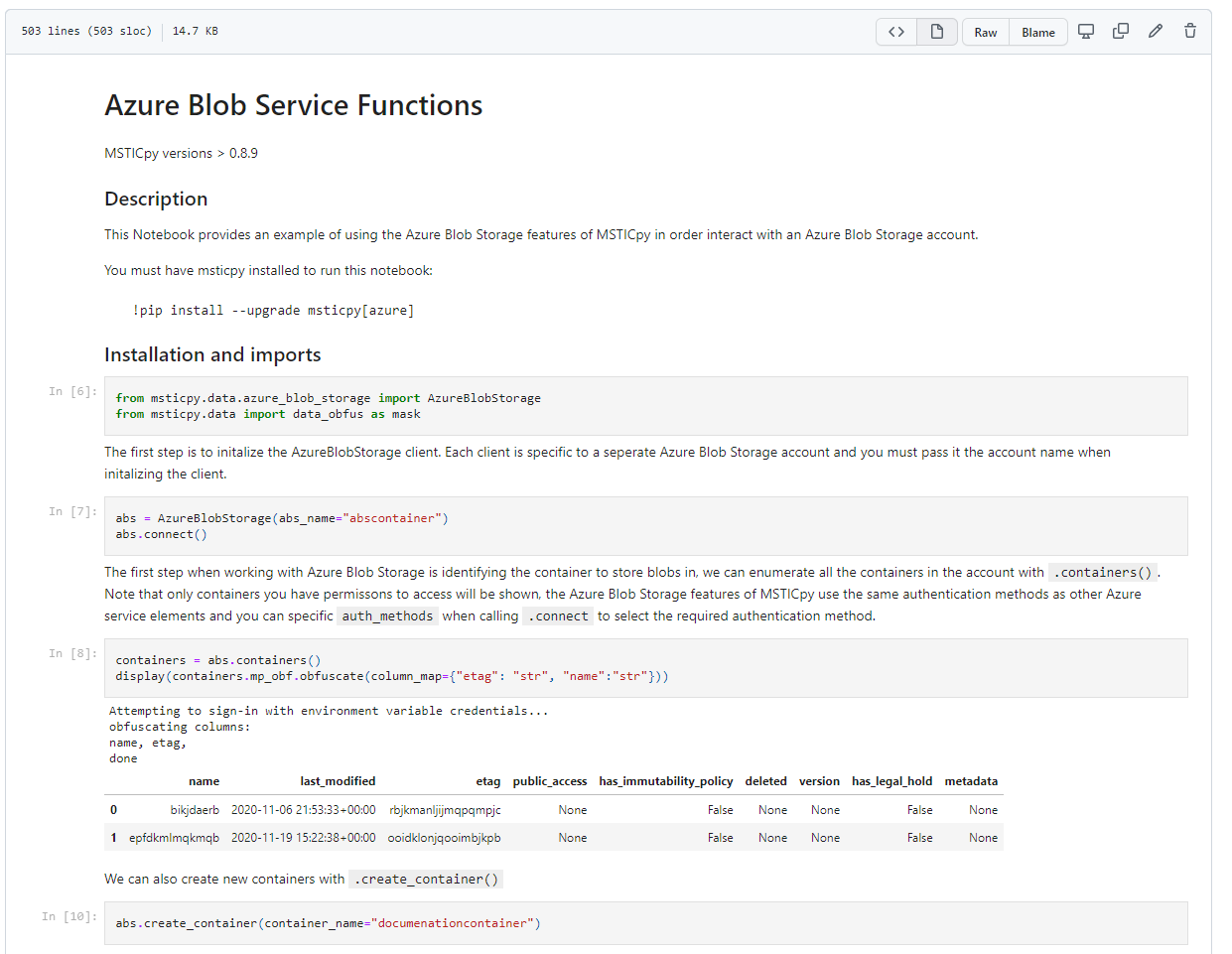
GitHub
GitHub provides a free, source-control-backed way to store notebooks (and other files), share your notebooks with others, and work collaboratively.
If you’re looking for a way to share your projects and collaborate with others, GitHub is a great option.

 Visual Studio Code
Visual Studio Code
